REVIEW: Mindstorms, by Seymour Papert

Mindstorms: Children, Computers, and Powerful Ideas, Seymour Papert (Basic Books, 1980).

I go to some effort to teach my kids math at home, which means they’re generally a year or two ahead of whatever’s happening at school. Most of my reasons are personal and idiosyncratic: I like math, and it’s fun to share my hobbies with my kids. I also despise the way math is usually taught, and do not want their first encounter with certain beautiful ideas to be ruined by some teacher who doesn’t really understand them herself.

When people find out about this, they generally assume I have a different motivation. They assume that I’m doing it so my kids will get ahead. I have to laugh at this, because I am about the least Tiger Mom person ever. Like Jane, I believe that your kids will be fine pretty much whatever you do, and that a happy and relaxed childhood for both kid and parent far outweighs whatever micro-advantage they might obtain out of you drilling them for hours a day. I also think the data backs me up here — ever since Piaget we’ve known that there are threshold ages when particular cognitive capabilities come online. I have a friend who likes to say: “you can start potty-training your kid on their first birthday and it’ll take two years, or you can start on their third birthday and it’ll take two days.” I’m not actually sure that this is true of potty-training, but I think it might be for calculus.

Nevertheless, I do actually think I’m giving them a leg-up, but in a sneaky and roundabout way. Like every parent, I believe my kids are the most amazing and brilliant beings ever. But deep-down inside I know that, statistically speaking, they’re probably around the middle of the bell curve. The one-to-two year advantage in math that I’ve given them will crumble quickly — partly because the actual geniuses will shoot past them without much assistance, partly because it’ll just naturally get eroded by the rising waterline, and by the fact that it’s easier to learn algebra at twelve than it is at ten. But it doesn’t matter, because being temporarily advanced at math will cause them to seem like the smartest kids in their class, even if they’re totally average. This will cause their teachers to treat them differently, and crucially, might cause themselves to think of themselves differently. And I have a hunch that that could turn out to be a much more durable advantage.

Yes, I’m one of those “growth mindset” people. I know that’s terribly unfashionable these days, and that everybody else who writes pseudonymously on the internet is very excited about innate differences in ability, and IQ tests and stuff like that. I used to believe an extreme version of the innate intelligence theory, and have written before about how it crippled my intellectual development through college. Two things happened that changed my views: the first was that I dug myself out of that epistemic hole, and noticed an immediate and commensurate improvement in my own abilities. That really got my attention. I was pretty sure that intelligence was innate, and yet changing my beliefs about the world and the ways in which I approached the world had made me smarter in all the ways that mattered.¹ If I could make myself smarter or dumber by changing my beliefs and my behavior, then presumably everybody else could too.

The second thing that happened was that the smartest person I knew told me that he thought intelligence was learned. His argument went something like this: over the course of your life, you pick up cognitive tools that make you more effective. Nothing shocking yet, everybody knows that there are kinds of knowledge that make you stronger at problem solving. This is the “standing on the shoulders of giants” effect, and it’s why you can solve harder math problems than the most genius caveman could. Psychometricians sometimes refer to this as the distinction between “fluid” and “crystallized” intelligence, and even the most hardcore believers in innate intelligence accept this. After all, a computer’s effectiveness is a product both of the raw capabilities of its hardware and the efficiency of the program it’s running.

But, my smart friend continued, there is another kind of cognitive tool you can pick up: meta-tools, deep lessons about the epistemic structure of reality or the contingent structure of your own psyche — tools which don’t make you better at any particular thing, but make you better at getting better at things. Recursive self-improvement, of the sort the AI doomers fear, right there at all of our fingertips, there for the taking. These meta-tools come in many different guises, I wrote about a few of them in my review of The Education of Cyrus, and I’ll mention a few more of them over the course of this post.² But the most important thing might actually be to avoid their opposite: the self-defeating beliefs or practices that make you dumber. One look at a drugged-out zombie camped by the sidewalk tells you that these must exist, but there are other IQ-lowering memes that are more subtle and insidious than meth addiction.

I think one common one is “I’m bad at math,” and that this is a terrifyingly easy trap to fall into and a terrifyingly hard one to dig out of. All it takes is one really bad explanation from a teacher at an early age, or one unlucky examination taken on a day you were coming down with a cold. We’re so conditioned, both as individuals and as a society, to believe that people are bundles of immutable aptitudes, that once the “I’m bad at math” meme enters our minds it can take root, grow stronger, and defend itself against attempts at exorcism. If I’m convinced I’m bad at math, then I might not bother studying for my math test, or I might choose to interpret the normal obstacles and frustrations of learning a new subject as evidence of my innate deficiency. I then do badly on my test, which further entrenches my self-sabotaging belief, and so on in a vicious cycle.

This is the problem that Seymour Papert wanted to solve. And whereas I am a cynic and only dare solve it for my own kids (by tricking both them and their teachers no less), Papert was a utopian and wanted to solve it for all of society and especially for the disadvantaged. This approach fits both his background (Papert was born in South Africa and spent a while as an anti-apartheid activist), and his intellectual milieu: the frothy, early years of the MIT AI lab. Was there ever a more optimistic time and place than Cambridge, Massachusetts in the middle of the 20th century? Cyberneticists were busy laying bare the nature of reality, rearchitecting human civilization, and preparing mankind for a new destiny of galactic colonization. So Papert set his sights on the comparatively easy project of solving education, once and for all. And naturally the best way to do this was by making a new programming language.

If that last paragraph sounded snarky, it really wasn’t meant to. Yes, judged by his own standards, Papert’s quest ended in failure, but at least he failed while daring greatly. The contemporary versions of Seymour Papert would never dream of doing something as wild and unhinged as fixing the educational system, and so instead they toil away inside of Google, optimizing click-through conversion rates and training neural networks to beam advertisements directly into our tooth fillings. By the standards of his time, too, Papert was great. Most of the 1960s utopians produced nothing but garbage, or occasionally something clever but evil. Papert’s book, on the other hand, is full of great ideas. And if with the benefit of hindsight we can see that he made a few giant mistakes, well, we should all be so lucky that in the end, we turn out only to have made a few.

To understand why Papert thought he could fix education with a new programming language, we first need to understand his theory of learning. Have you ever noticed that there are two very different kinds of “knowing” something? There’s the kind where you can parrot an explanation somebody else gave you, but the details are all a bit fuzzy, and you would quickly fall apart under questioning. Then there’s the kind where you inhabit the knowledge, it’s like an old friend or like the neighborhood you grew up in, you know its strengths and weaknesses, where it came from, how it got to be that way, and where it’s probably going. If a reality TV show ambushed you in a restaurant and told you to stand up in front of the live cameras and give a 5-minute lecture on the topic, you would be terrified if you had the first kind of knowledge, and totally at ease if you had the second kind. More importantly for education, the first kind of knowledge is ephemeral, you’ll forget it over the summer. But the second kind makes a strong foundation or structural element in the great epistemic cathedral that we all should be building.

Papert was a student of Piaget’s, and hugely influenced by the latter’s theory of constructivism. Roughly speaking, constructivism says that the first kind of knowledge, the shallow and fuzzy sort, is what you get by memorizing or absorbing new information. The second kind is only produced when the student is actively creating or reframing their own internal mental models in their own language. This happens all the time in math education. I can think of many occasions where I had a mathematical concept explained to me, but didn’t really “get it” until I had built up my own explanation with my own terminology, motivating examples, and mental images. Even if you didn’t get very far in math, I bet this happened to you, or I hope it did! Maybe your teacher was explaining long division to you over and over and over again, and it never made any sense, until one day you explained it to yourself, and told it in terms of a silly story with meaning to nobody but you, and in doing so you took it apart and put it back together, and then “click!” you had it forever. Constructivism says all true learning is like that.

I totally believe it, and this is one reason why when it comes to teaching math I’m such a fan of the Moore method, which uses Socratic questioning and guided exploration to lead the student to invent a theory or a technique him- or herself. But I think constructivism is also true in many subjects besides math. Our understanding of the world is like a huge collection of overlapping maps. When we memorize a new fact in isolation, it’s shaky and ephemeral, it can easily get blown away, we don’t see the connections. When we fit the new fact into a map, “click!”, it snaps into place, it makes sense, everything around it helps to hold it in place, and if you momentarily forget it, you still know where to look because you know what it’s “near.” Sometimes the maps can be literal, like when we’re learning geography, or a historical timeline. Somebody might tell you, “it happened in the 1470s,” and that might mean nothing to you. Or somebody might tell you, “it happened in the 1470s,” and you instantly start thinking about the fall of Byzantium and the discovery of the New World, and the Ming dynasty, and so on. In the second case, the fact is more meaningful, more contextualized, and you’re a lot less likely to forget it.

But a key ingredient in being able to build these models is having a rich “vocabulary” of primitive concepts to piece together. In some cases, like the historical timeline example, that vocabulary is mostly just other facts. But more commonly, it’s something closer to a set of idioms and references and sense-memories that are completely personal. Here’s an example Papert gives:

Before I was two years old I had developed an intense involvement with automobiles. The names of car parts made up a very substantial portion of my vocabulary: I was particularly proud of knowing about the parts of the transmission system, the gearbox, and most especially the differential. It was, of course, many years later before I understood how gears work; but once I did, playing with gears became a favorite pastime. I loved rotating circular objects against one another in gearlike motions… I became adept at turning wheels in my head and at making chains of cause and effect.

…

I believe that working with [gear] differentials did more for my mathematical development than anything I was taught in elementary school. Gears, serving as models, carried many otherwise abstract ideas into my head. I clearly remember two examples from school math. I saw multiplication tables as gears, and my first brush with equations in two variables immediately evoked the differential. By the time I had made a mental gear model of the relation between x and y, figuring how many teeth each gear needed, the equation had become a comfortable friend.

Papert goes on to note that no educational researcher, no experiment, no test would have discerned that when he was two years old a key conceptual breakthrough occurred that would influence his mathematical career forever after. One thing that’s so cool about this vision of education is that it makes it extremely personal. The entire process of learning is about the student discovering the fact anew, and relating it to ideas and memories and analogies that won’t work for any other person. But the flip side is it suggests an incredibly daring way to make education easier: we simply have to create a richer conceptual vocabulary for every human being on the planet. So that’s what Papert decided to do.

The reason Papert believed that there’s low-hanging fruit here is that he looked around the world, and saw that there were certain things that children everywhere, from New York City to Papua New Guinea, learned with ease. These things included counting, various conservation laws (if you pour water from a short and wide glass into a tall and skinny glass, the amount of water doesn’t change), and the kinds of geometry useful in somatosensory processing. But conversely, there were other things that children everywhere had great difficulty learning; for example certain kinds of abstract symbolic manipulation, formal logic, and so on. From these observations, he concluded first that all human cultures share a basically identical set of mental models and conceptual tools, and second that they’re all equally deficient in another set of mental tools that are useful for abstract and algorithmic thinking.

To be clear, I think this was a totally insane conclusion, and the first of Papert’s two big mistakes. His thinking on this was strongly influenced by Piaget’s experimental results on early childhood learning, which showed that certain cognitive techniques and abilities are learned at almost identical ages across cultures. But it seems to me that a much more economical interpretation of Piaget’s results is that these abilities are mostly innate, or at least biologically gated, and come online after age-dependent phases of brain development.³ Similarly, the fact that nearly all children struggle with abstract logic games can be taken as evidence that our ability to do logic is not innate, but rather the result of using our verbal reasoning in a way that nature never intended.⁴ I have no idea why Papert instead settled on his strained cultural interpretation, other than the fact that it was the 60s and cultural explanations were in vogue.

Nevertheless, we should be grateful for his wrongness, because it led him to do something awesome. Papert’s diagnosis is that higher math and computer programming are hard because their mental building blocks aren’t in wide social currency (he observes, for instance, that concepts that are second-nature to every programmer, like “a loop nested inside another loop” and “debugging” are not part of society’s shared vocabulary). The solution then is to build a bridge, from the familiar and intuitive world of bodies, movement, and common sense, to the unfamiliar world of abstraction. An incremental, step-by-step progression that starts with objects that are very familiar, and grounds a growing mental vocabulary for abstraction in the categories of everyday life.

But this isn’t just about teaching kids to code, because the really crazy ambition is that by teaching them to code he can teach them everything else. Literally everything. Papert asserts that by programming a computer, one is forced to reflect on the act of thinking itself, and that doing so forces you to build for yourself some of the “meta-tools” I mentioned that make you permanently smarter and better at solving every other kind of problem. For example: computers execute instructions step-by-step, so when a computer program goes haywire, a natural thing to do is to imagine oneself as the computer, executing the instructions and thinking about what you would do at each step. But the technique of “think about it step-by-step and try to find the step that goes wrong” is actually useful in many domains besides computer programming! He gives a ton of examples besides this one, and what they all have in common is that they’re generally useful, easy to learn while playing around with computers, but not obvious to a surprisingly large number of people.

Here’s a different analogy for the same (totally crazy) claim. In Papert’s childhood, a set of gears became a piece of mental scaffolding that countless difficult concepts and techniques would later come to hang off of. But the computer is infinitely protean. It can become a set of gears, it can become anything, it is a “machine for thinking,” and by interacting with it as a builder and creator, you are tricked into building very powerful and general-purpose thinking tools for yourself. So putting it all together, Papert’s goals are: (1) make learning to program computers as easy and intuitive as learning to dance, by building a bridge from the physical world to the abstract world, and (2) by teaching kids to program computers, make them learn to think better, and learn to learn better.

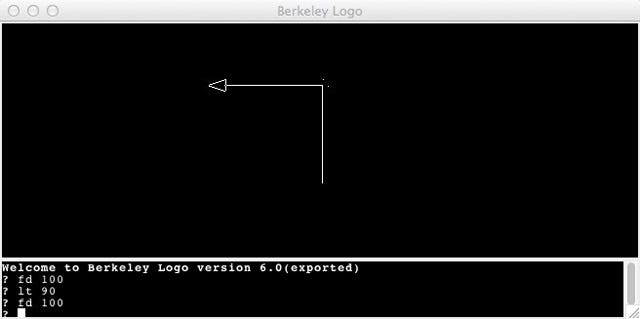
Papert spends most of the book explaining his “bridge,” a now-legendary visual programming system called Logo. Logo programs comprise a series of commands given to a virtual, computerized turtle (yes, an actual turtle). The commands which come pre-defined in the language are extremely concrete — like “RIGHT 90”, which causes the turtle to turn, or “FORWARD 100”, which causes it to advance in the direction it’s currently facing. As the turtle moves, it leaves a line behind it, so the sum of the turtle’s movements draw a picture. But even a very complicated Logo program ultimately boils down to a list of these fundamental movements. The reason Logo serves as a good “bridge” is that one end is firmly planted in things you do every day — walking forwards, walking backwards, turning your body. The novice Logo programmer imagines him or herself as the turtle,⁵ going through the same motions in the same order, like a set of dance instructions. Debugging this system looks like asking the question: “how did I end up standing over here instead of over there”, and that is a much more natural question for a human being to think about than some tricky logic puzzle.

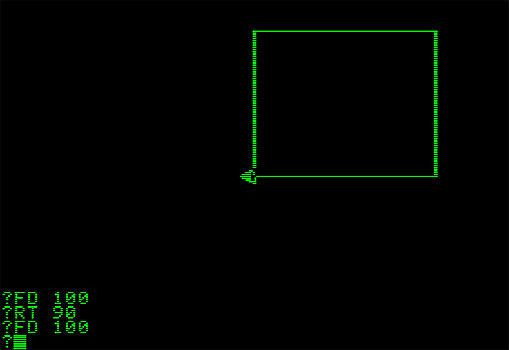
So far so concrete, but the purpose of Logo is to be a bridge from the concrete to the abstract, so it also has lying around all the tools needed to fashion repeatable building blocks, and to compose those building blocks into intricate and complex creations. Rather than force these abstractions down the budding programmer’s throat, Logo attempts to harness the natural curiosity, and crucially the natural laziness of a child to its educational advantage. For example, the first time the child wants the turtle to draw a square 100 pixels wide, he may type the sequence of commands: “FORWARD 100; RIGHT 90; FORWARD 100; RIGHT 90; FORWARD 100; RIGHT 90; FORWARD 100; RIGHT 90”. But already the second time the child wants to draw a square, typing all that out again is annoying, and the third time it’s intolerable. So the child reaches for a set of tools one level more abstract, tools that let him teach the turtle “this is what it means to draw a square,” to add that concept to the computer’s vocabulary, to bind it to a name: SQUARE. So SQUARE becomes a shorthand for that whole set of instructions, and the child can move on to more complex creations comprised of many SQUAREs. And, crucially, the child may also have done some deep reflection on the nature of the world, of teaching, of thinking, and of squares.

This is a very basic example, barely one step above the brute physicality of “FORWARD 100.” Logo offers many such steps. Computer scientists sometimes use the metaphor of a “ladder” extending upwards towards greater complexity and abstraction, but Logo’s ladder is more of a gentle ramp. And even the loftiest and most rarefied Logo program ultimately boils down and bottoms-out into a finite and concrete list of simple geometric instructions that can be acted out or played through with body movements. Over the course of developing Logo, Papert worked with hundreds of children and watched them progress up the ladder of abstraction. Many of these were not “smart” children: some of them were “problem” children, children who had intellectual or behavioral or attention or motivation issues in school. And Papert tells story after glowing story of how these kids figured it all out, progressed up the ladder, then went back to school and saw their problems melt away. They were changed by the experience of learning Logo, something had been unlocked deep within their minds, and they now ran circles around their former classmates. These stories are gripping, but they raise a troubling question: if Logo works so well, why didn’t it take over the world? Why didn’t it fix education? I think I have the answer.

Reading this book stirred some ancient memories deep within me, which came back first hazily, then with devastating clarity.⁶ I WAS TAUGHT LOGO AS A CHILD! I had totally forgotten this ever happened, but after reading this book I am certain. Sometime in elementary school, my whole class spent a couple of days commanding the digital turtles on ancient, thrumming CRT displays in a computer lab with faded brown carpets. But something didn’t quite jive between Papert’s proud description of the system he’d created, and my own memories of using it. In the Logo I remember, there was no ladder of abstraction. In fact there was no abstraction at all. We commanded the turtles with our simple, linear sequences of commands. We steered them around corners, and through mazes. We got very good at estimating numbers of pixels and how many degrees of rotation it would take to go around an oddly-shaped corner. But there was no abstraction, no creation of virtual worlds, no expanding conceptual vocabulary, no production of mental scaffolding.

Was I exposed to a defective version of Logo? I don’t think so, since as far as Google will tell me there is no such thing. I didn’t have defective software, I had a defective teacher, one who had no idea what the point of this educational software was, and who might even have actively concealed the point from us lest we get confused. The magic lamp was sitting there with all its power, but rather than making wishes, we used it to play soccer.

What if the reason Papert’s test subjects experienced an intellectual transformation had nothing to do with Logo or turtles or any of that, and everything to do with the fact that a kind, patient, and brilliant adult was devoting his full attention to helping them learn? Many geniuses have this one thing in common: they were individually taught by accomplished private tutors. Papert spends much of his book refuting criticisms that his methods are impractical because they require every child to own a computer. He was right about that: today every child carries a computer in their pocket. But those computers do not play Logo, they play TikTok. Papert’s greatest mistake was misunderstanding the nature of scarcity. Computers are cheap. The thing that’s hard to find is adults who are both willing to devote themselves to teaching the next generation, and smart enough to do a good job.

1. I’ve never taken an IQ test, so I don’t know whether my scores before and after my intellectual transformation in my mid-20s. I also don’t much care. My ability to solve problems, including very abstract problems, and my ability to deploy my cognitive capacities to advance my objectives both took a big leap. In fact I prefer to define intelligence as something like, “how effectively you can use thinking to achieve your goals”. I’ve never heard a different definition that wasn’t either self-referential or trivial.

2. The kind I’ve personally been working on lately is a form of somatic knowledge that I sometimes think of as “getting good at piloting the mind.” We’re all born and grow into these bodies, and they don’t come with an owner’s manual. Just like a jet engine functions best with fuel within a relatively narrow octane range, there are particular diets, exercise regimens, sleeping patterns, times of day, and environmental stimuli that are especially conducive to deep cognitive work. But the exact settings are different for every person, and one of the few silver linings of aging is you both begin to figure out what your own optimal operating parameters are. For me the difference between exhausted and well-rested is at least 20 IQ points, maybe more, so this is a very concrete way in which you can make yourself smarter. What’s fascinating about it is the way in which it straddles the line between “know-how” and “know-that”. Part of it is about learning a set of facts about yourself, but part of it really is more like becoming a more fluid and professional driver.

3. As far as I know, this was Piaget’s own interpretation of his data.

4. The ability of large language models to engage in a clunky sort of logical reasoning after being trained to produce language may be further evidence for this hypothesis.

5. Here we see the wisdom of making it a cute animal, the programmer’s mirror neurons are firing!

6. It would come as no surprise to Proust that it wasn’t any part of Papert’s descriptions that stirred this memory, but rather direct sensory information: the blocky, pixelated turtle icon, and the look of the all-caps command sequences.