REVIEW: Math from Three to Seven, by Alexander Zvonkin

Math from Three to Seven: The Story of a Mathematical Circle for Preschoolers, Alexander Zvonkin (Moscow Center for Continuing Mathematical Education, 2007).

To me, one of the greatest historical puzzles is why the Cold War was even a contest. Consider it a mirror image of the Needham Question: Joseph Needham famously wondered why it was that, despite having a vastly larger population and GDP, Imperial China nevertheless lost out scientifically to the West. (I examined this question at some length in this review.) Well, with the Soviets it all went in the opposite direction: they had a smaller population, a worse starting industrial base, a lower GDP, and a vastly less efficient economic system. How, then, did they maintain military and technological parity¹ with the United States for so long?

The puzzle was partly solved for me, but partly deepened, when those of us who grew up in the ‘90s and ‘00s encountered the vast wave of former Soviet émigrés that washed up in the United States after the fall of communism. Anybody who played competitive chess back then, or who participated in math competitions, knows what I’m talking about: the sinking feeling you got upon seeing that your opponent had a Russian name. These days, the same scenes are dominated by Chinese and Indian kids. But China and India have large populations — the Russians were punching way about their weight, demographically speaking. Today, those same Russians are all over Wall Street and Silicon Valley and Ivy League math departments, still overrepresented in technical fields. What explains it? Are Russians just naturally better at math and physics?

When I related these questions to an Ashkenazi-supremacist friend of mine, he immediately suggested that “maybe it’s because they’re all Jewish.” (I’ve noticed that the most philosemitic people and the most antisemitic people sometimes have curiously similar models of the world, they just disagree on whether it’s a good thing.) My friend’s question wasn’t crazy, since there are definitely times when asking “were they all Jewish?” yields an affirmative answer. But in this case I had to disappoint him with the knowledge that many of these Russian math and chess superstars were gentiles.² What’s more, by the ‘60s and ‘70s the Soviets had an entire discriminatory apparatus dedicated to keeping Jews out of the scientific establishment, so it would be impressive indeed if they were the foundation of its success.

Another possible explanation actually hinges on the relative poverty of the Soviet Union. Assume there are a lot of people out there with natural mathematical talent, but who given their druthers would major in underwater basket-weaving instead. The United States, because it’s so wealthy, can afford to “waste” a huge proportion of our talented population on humanities, arts, and other stuff that doesn’t involve you sitting in the school library until 3am. In other words, not going into a technical field is a form of luxury, which America can afford to consume. The Soviets, rather like the Chinese today, were forced by their underdog status to allocate human capital more efficiently (and had the authoritarian means to do so by force if necessary). This theory is related to the curious fact that, on average, the more feminist your society, the fewer women there are in math and science — which makes total sense if you assume that on average women are good at math but uninterested in it.

The thing is, the émigré superstars I encountered didn’t seem at all grudging or resentful about their studies. If anything it was the opposite. I’ve previously complained about how much I hate Russian mathematician Edward Frenkel’s³ book, but one thing it gets across well is just how important passion is to being a great mathematician, and passion was the thing the émigrés seemed to have a surfeit of. In college, the joke was that seminars by American professors would last an hour, whereas seminars by Russian professors would turn into boisterous debates lasting all night. People have been writing for centuries about Russians having a tendency towards “maximalism” — whether aesthetic or ideological or anything else. Maybe a culture-wide commitment to not doing anything by half-measures explains it?

These are all fun theories, but in the interviews I’ve read with Soviet mathematicians and scientists, the things that come up over and over again are “mathematical circles,” a practice that originated in the pre-revolutionary Russian Empire and then spread far and wide through the Soviet Union. A mathematical circle is an informal group of teenagers and adults who really enjoy math and want to spend a lot of time thinking and talking about it. They’re a little bit like sports teams, in that they develop their own high-intensity internal culture and camaraderie, and often have a “coach” who is especially talented or famous. But they’re also very unlike sports teams, because they don’t compete with each other or play in leagues or anything like that, and usually any given circle will contain members of widely varying skill levels. Maybe a better analogy is a neighborhood musical ensemble that gets together and jams on a regular basis, but for math.

The most important thing to understand about mathematical circles is that the math they jam on is completely unlike the math you study in school, and also completely unlike the “competition” math that bright kids in the United States sometimes do. Both school math and competition math are primarily comprised of exercises. An exercise is a question concocted by a human being for a didactic purpose. Any bright kid with any amount of genre-savviness can immediately make a few assumptions upon being assigned an exercise. He or she can guess that the exercise is solvable in fewer than five minutes with the appropriate techniques, and that it is related to the material in the current chapter of the book. A clever student can often use psychological techniques to reverse-engineer what the teacher or the designer of the standardized test was trying to get at with the exercise, and answer it through a process of elimination or savvy guessing or pattern matching.

Solving an exercise is like hunting a neutered zoo animal. It may be a low-stress environment for polishing particular aspects of your technique, but it will not help you to survive in the wilderness. For that, you need to see people solving problems. A problem is a question of interest that comes up when somebody is trying to do something real. A problem may not be solvable by you, or by your coach, or by any human being. Even if the problem is solvable, it may require weeks or months of dedicated, painful pursuit. It may not be obvious what techniques are required to solve a problem, they may not be techniques that you know, or it may require a surprising combination of techniques. The problem is mathematical nature red in tooth and claw. There are no guardrails. There are no hints or answers at the back of the book. There is no book. It may eat you.

(For more on exercises vs. problems, read my review of The Education of Cyrus.)

The bread and butter of the mathematical circle is solving problems together, as a team. There is no time here for exercises; you can do that lame stuff at school. Sometimes the coach picks a problem for you, something just beyond your ability, just the thing you need to hone your edge. But sometimes the whole circle works together on a problem that nobody has the answer to and that challenges the very best members. These problems are the most important, because with them you see great minds, men older and more talented than you, stretched to the breaking point and occasionally beaten. You see them grind and grind and try every possible attack on a problem and sometimes lose anyway. And you see them not run from being defeated, but cheerfully charge in again, because losing is good for you, losing is how you know you’ve picked an opponent worthy of a man. You learn to love things that are hard. And occasionally you win, and when you win it feels like you all win, like humanity wins, because you’re all in it together, all doing something beautiful and dangerous and exemplary of the best qualities that human beings have.

There are also times when everybody is too tired to work on a problem, and in those moments of recuperation, it’s the coach’s job to tell stories of legendary problems of the past and of the mathematicians who slew them. These stories often contain lessons, inspiration, or perspective on how mathematics evolved and got to be the way it is. Human history would look very different, after all, without the brachistochrone problem or the roots of a quintic polynomial problem or the icosahedron problem or the precession of Mercury’s perihelion problem. But other times there’s no hidden lesson, no grand perspective on the human story. They’re just ripping good yarns, and hearing them is a process of initiation into mathematical folklore, because every culture (and mathematics is surely a culture) has shared stories and references and inside jokes, even when they’re purely for fun.

This book is the story of one such mathematical circle. But it’s an unusual one because…it’s for preschoolers.

The “coach” of this circle is Alexander Zvonkin, a professional mathematician frustrated that his kids are having all the wonder and life and joy crushed out of them by the grey functionaries at their school. So he starts a circle for his son Dmitry and a few of the neighbors’ kids, most of whom are around three or four years old. That’s young enough that according to Piaget’s experiments there are cognitive modules related to number and volume that simply haven’t come online yet. Fortunately, Zvonkin is familiar with the latest research on developmental psychology, and turns lemons into lemonade by using the kids’ lack of numerical intuition to introduce them to some pretty deep ideas about when two sets have equal cardinality. (If you’re curious, he talks more about these experiments in this journal article.)

At this point I expect you are rolling your eyes, especially if you have experience with three-year-olds. It can be difficult enough to get them to sit still, never mind ponder deep questions about the cardinalities of sets. And what exactly does it look like to pit somebody against a problem who is barely potty-trained? This is where the genius of Zvonkin’s format kicks in — it’s not really a book, it’s a journal, and one that is barely edited. So it’s full of failure after failure, entries like, “today I had a cool idea for a puzzle but everybody just screamed instead and then one of the kids vomited.” And yet, slowly, wondrously, over the four years of the circle’s existence, his patience pays off and the kids start doing really incredible things.

His initial goal, when the kids are at their youngest and are least prepared to match wits against a problem, is just to counter-program their schoolwork a little bit. Zvonkin hates the fact that their school presents math as a set of formulas to be obeyed, and DESPISES the fact that the kids’ midwit teacher deducts marks for failing to write answers in a designated format.⁴ Worst of all, the teacher docks points when the kids use techniques that they “aren’t supposed to know yet.” So Zvonkin throws himself full-bore into discomfiting and unsettling the pat answers they’re bringing home from school, emulating Socrates both in his methods and in his singular focus on corrupting the youth.⁵

About a year into this, Zvonkin decides that the kids are ready for their first real problem, and asks them the following simple question: how many ways are there to select two items from a collection of five items, if the order in which they’re chosen doesn’t matter? This is a question from the field of combinatorics, which Zvonkin notes with a sneer used to be taught to advanced high-schoolers, until the authorities decided it was too hard. And here he’s going to teach it to preschoolers, or, even harder, he’s going to make them figure it out for themselves with very few hints.

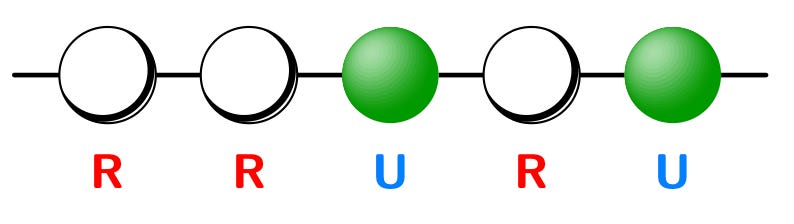
He does this, maddeningly, by showing them the problem over and over again, in many different guises and disguises, over a period of months. He does it inductively, because four-year-olds are tactile creatures who have not yet assembled the cognitive tools required to reason formally and symbolically (more on that in my review of Mindstorms). First he gets beads and asks them to make chains of two red and three blue and asks them how many possible such chains there are. A boisterous debate follows: if you take a chain and rotate it 180 degrees, does it count as the same chain or a different one? This is a good mathematical question, and Zvonkin gives the mathematician’s answer: “We can make up the rules, we can decide whether it counts, so now we have two problems instead of one, but it turns out that one of them is both easier to solve and more interesting.”

The kids have fun with their beads, but they are still nowhere near ready for the theory of how to count ways of choosing k items from an n item set. That’s okay, he’s just getting started. He lets a few months go by, he lets them forget it, then he gives them sheets of paper with rows of five circles, and challenges them to find as many different ways as possible of coloring just two of them. As the kids are coloring, he asks if this reminds them of anything… they pause. There’s something in the backs of their heads, but they aren’t sure. It’s getting closer though.

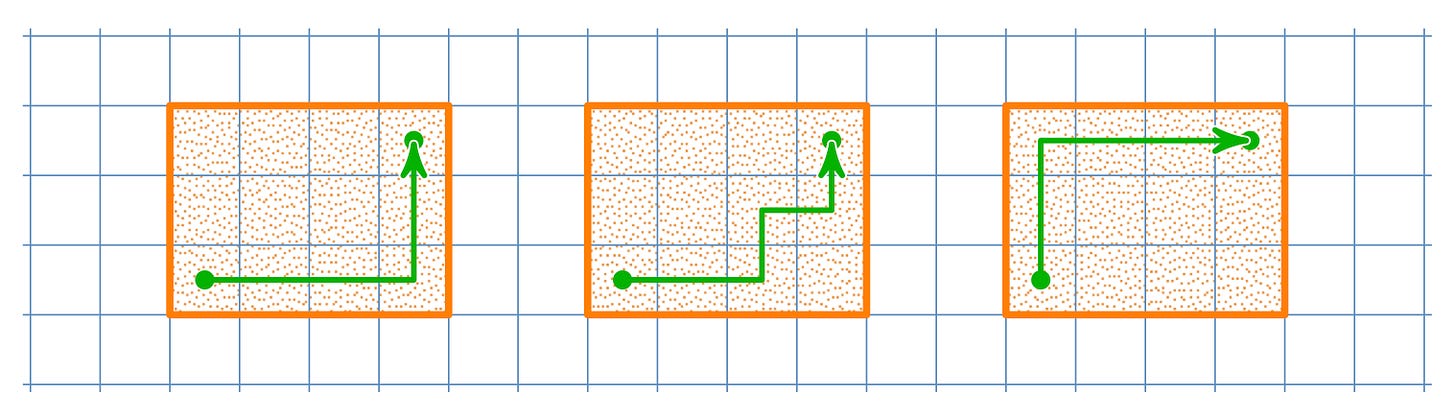
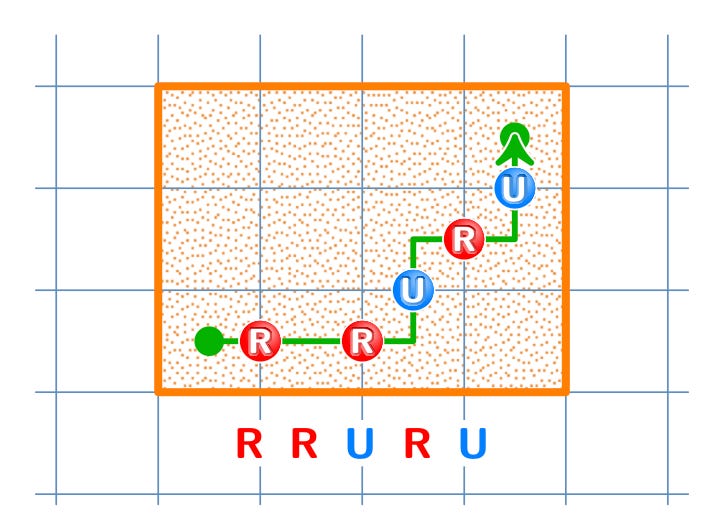
More months go by, and it’s time for the problem to visit again. This time he brings a 4x3 grid, and explains that it’s a city map, and that a taxi is starting in the lower-left corner, and wants to go to the top-right corner, and asks how many possible paths it can take with no backtracking. Once again they leap into action. Once again he asks if this reminds them of anything. The kids are confused, they’ve never played the taxi game before. This time he drops a hint, takes one of their paths, and each time the taxi makes a decision to go right, he draws a little red circle, and each time it goes up he draws a little blue circle. Pandemonium. The kids are going nuts. They have discovered the beauty of isomorphism, a secret passage leading from one part of the world, up into the Platonic realm, and back into another superficially very different place. But they still haven’t answered the problem.

He lets a couple more months go by. Now he places five empty matchboxes and two balls on the table. How many different ways are there to put the balls in the boxes? This time the kids figure it out quickly: it’s the same as the puzzle with the beads! And that means they’re finally ready to stare the problem in the face, ready to begin their ascent of this mountain. The answers to all of these puzzles, which are really all the same puzzle in different clothing, is that there are ten ways. But if we enumerate all ten of them, how can we prove that there aren’t any more? And what if our original set had four items or six items instead of five, how would the answer change? And these little kids who don’t yet know their times tables will totally figure it out.

What should we expect from children intellectually? Are they, as Piaget says, neurologically incapable of certain kinds of thought? Or are they, as Zvonkin believes, capable of solving challenging problems that many adults would struggle with? I think the answer is “both.” There’s a persistently wrong belief that many people, even many teachers, implicitly or explicitly hold, which says that children are basically like adults, only they’re dumber and know less stuff. Call this the “homunculus theory” of childhood cognition. But the truth is that kids are more like artificial neural networks — they’re at a subtly different point in mind-space, they’re good and bad at different things than adults are good and bad at.

For example: young children are much more concrete thinkers than adults, whether that’s for neurological reasons or because they haven’t built the cognitive tools for abstraction yet.⁶ When you meet an adult who can’t reason symbolically or propositionally, they’re often (though not always!) pretty dumb and bad at thinking in general. What a mistake it is to apply the homunculus theory and assume the same of a child. You’ll underestimate and condescend to them and cheat them of opportunities to figure things out for themselves, while simultaneously getting frustrated at their inability to grasp incredibly simple ideas. They aren’t homunculi, they aren’t tiny adults, they’re an intelligence that is differently shaped from yours. This is an unintuitive and uncomfortable idea for us, and we don’t have the mirror neurons to really grok it, but consider it good practice for all the very strangely shaped intelligences we will be encountering in the coming decades.

One thing Zvonkin does that works about equally well on kids and adults is repeating things over and over again, and letting a long time go by between the repetitions. The reason this works is the same reason that when I’m trying to figure something out for myself, I’ll think about it really hard for a while and then go for a walk or take a shower. You’re hijacking the interplay between the focused-mode and the diffuse-mode of cognition (which I discussed in a review of a book by Hillaire Belloc, of all people). It works even better if on each repetition you come at the problem from a different angle, so your subconscious has new material to chew on. Using this technique I was once able to get a five- or six-year old to figure out why summing the numbers in any row of Pascal’s triangle must give a power of two.⁷

The most important lesson of Zvonkin’s book, though, and also the realest and the rawest, comes at the end. He’s been running his little circle for four years, has racked up triumphs and failures, formed all sorts of theories about how best to teach math to little kids, and recorded it all in gory detail. That last is important, because his daughter Evgenia is now a little older than his son Dmitry was when he started the original circle, so naturally he decides to do it all over again with Evgenia and with the neighborhood kids who are her age. But this time, he’s armed! He already knows what works and doesn’t, he has handwritten journals full of hard-won lessons, he’ll be able to save a ton of time and run everything much more smoothly.

As if. In the second iteration of the circle, all of his notes are completely useless, and all of his initial attempts to teach anything fail, because these are different kids with different aptitudes and different interests. Zvonkin, raised in a communist society and a believer in the absolute malleability of human nature, is fairly bowled over by this, especially by how young all these differences are manifesting. Reading between the lines, it sounds like he got quite lucky with his first set of children, and that the second group were much more challenging to teach.⁸ The most eloquent testimony to this is that after about a year he gives up, and the journal ends abruptly.

This is just an extreme version of the universal experience of being the parent of more than one child. The moment your second kid is born, or sometimes even before they’re born, they begin teaching you how little impact you actually had over the life trajectory of your first kid. The differences between them,⁹ despite the fact that you do almost everything the same, testify to just how much of parenting is actually a powerless process of watching a new being discover and disclose to the world what it is going to be. In one way, this makes what’s going on even more existentially dramatic — you’ve produced not a blank slate that you can program, but an alien intelligence that will produce a whole new universe.

The other thing is that despite being a tiny bit demoralizing, this is also tremendously liberating: your actions can only change who they are on the margin, so you can relax and do things that are fun for both of you. Sometimes that means a favorite book or movie, sometimes a love of sport or hiking. And sometimes, the shared activity that brings both of you joy is a love of thinking, even the strenuous sort of thinking that comes from wrestling with a problem.

1. There are scientific sub-disciplines where even at the end the Soviets had a clear lead, including several fields of math. Even crazier, there are sub-disciplines where we have not yet gotten back to where the Soviets were (for instance phage therapy).

2. Undeterred, my friend pointed out that many modern Russian gentiles have significant Jewish ancestry. The Soviets actively promoted mixed marriages, to the point where in some cities the average urban gentile Russian is as much as 25% Jewish. I still don’t think this explains Soviet scientific prowess, but it’s an interesting data point because the most highly urbanized areas are the ones where most of the mathematicians (and most of the emigres) came from.

3. Before you ask, I looked it up and Frenkel is half Jewish, half gentile. I will leave it to you whether you count that as evidence for or against my friend’s theory.

4. Interestingly, while he starts out full of fire and brimstone and sounding like Lockhart’s Lament, he later gets invited to teach an experimental math curriculum at a Moscow public school and comes away much more appreciative of the constraints that both teachers and administrators are working under.

5. There’s a weird echo here of what post-structuralist humanities professors think they’re doing with each new crop of undergrads. But of course what the professor is actually doing is reinforcing dominant paradigms and indoctrinating the next generation in the mores and dogmas of the official state belief system. Our society is simply so advanced that it conceals its official doctrine as a sort of radical skepticism (but only on approved topics).

6. Or maybe those are just the same thing.

7. The aggravating thing about how well this works is that…it means all those schools I hated were actually onto something. One of my least favorite things about elementary school math class was how it was the exact same thing every year. But actually if you have kids who are struggling to grasp a concept, just giving them many opportunities to attack it, with lots of space between them, might do a lot of the work for you.

8. Though interestingly, one girl from the second circle later became an actual mathematician as an adult.

9. A friend of mine once pointed out to me that assortative mating drastically increases variance in offspring. So if you’re similar enough to your spouse, say…to write a Substack with them, you may want to pursue diversification as a strategy with your kids.